近年では資産運用を見直す方が増えつつあります。その理由としては「老後2,000万円問題」などのニュース、低迷する経済状況などの影響が考えられます。また長引く低金利の時代は現在も引き続いており、「銀行に預けてもお金が増えない」という状態ゆえに投資などへ興味を持つ若い世代も少なくありません。
そこで今回は、投資をするうえで重要な「複利計算」について解説。
単利・複利の違いや複利計算の公式、複利で資産運用をした場合のシミュレーションなどもご紹介します。
単利と複利とは?それぞれの違い
そもそも「利息」「利子」とは、お金の貸し借りにおいて金額、期間に応じて支払われる“対価”を指します。また「金利」とは、1年単位で上乗せになるお金の割合をパーセンテージ(%)で表したものです。
自分が債務者(借りる側)となった場合は借りた金額に応じた利子を上乗せして返済をします。住宅ローンやカードローン、創業融資などを思い浮かべると分かりやすいでしょう。
一方、銀行への預貯金や株式投資やつみたてNISA、iDeCoなどの資産運用においては、元本に対し預け入れた期間や運用期間に応じて利息がつくことになります。
こうした金利の計算には「単利式」「複利式」の2種類があり、それぞれ異なる特徴を持っています。
【単利式・複利式それぞれのイメージ】
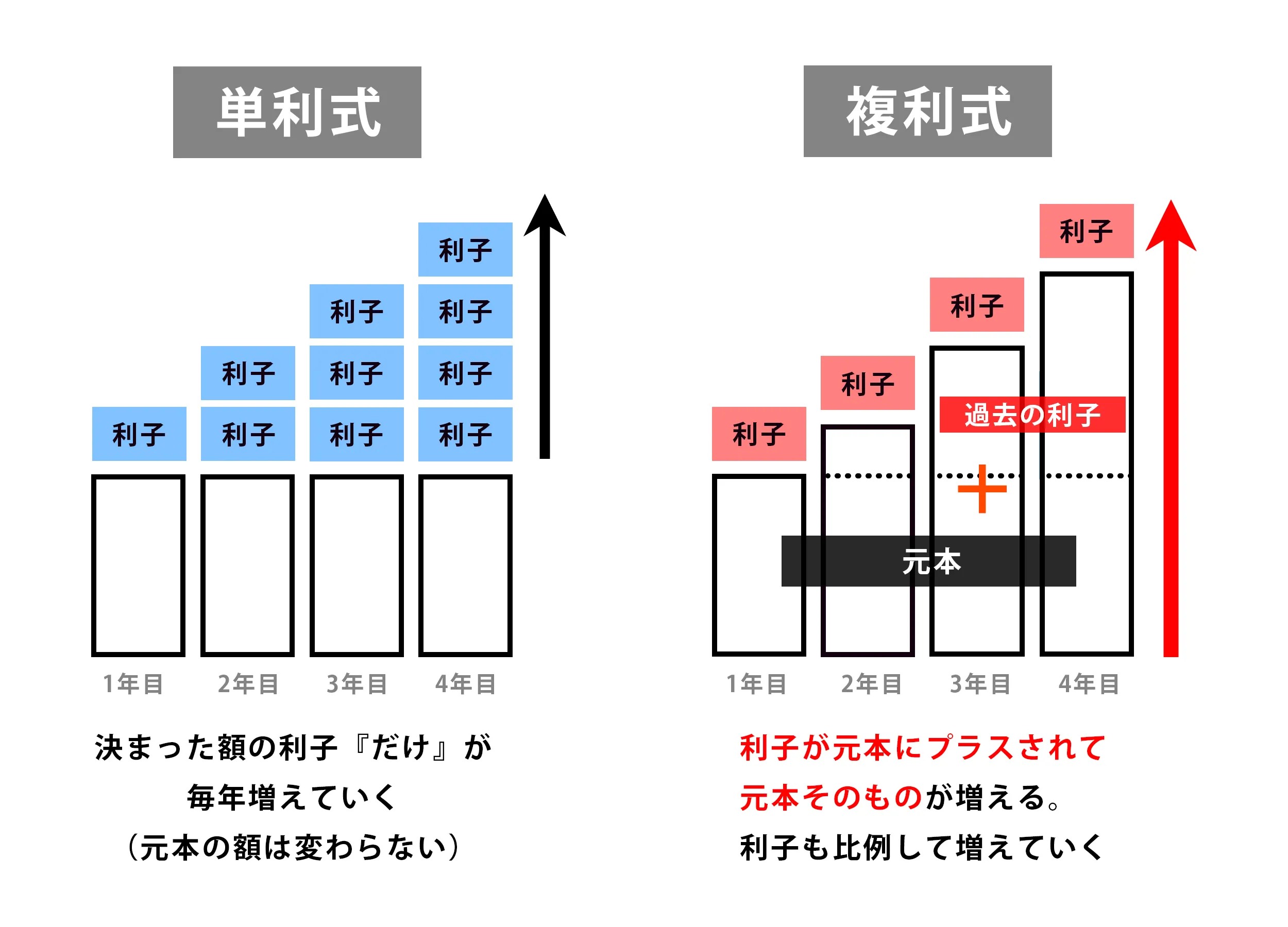
単利式とは
単利式とは、運用元本に対し毎年同じ金額の利子をつける計算方法です。
運用元本の金額は途中で追加しない限り同じで、利子も変更がなければそのままの割合で運用されます。
仮に10,000円の元本があり、毎年100円の利子が増えるとした場合、1年目は+100円、2年目は+200円、3年目は+300円……というふうに、利子だけが増えるイメージです。
単利はさまざまなお金のやり取りで活用されていますが、とりわけ「自分が運用する側」となった場合、以下のような金融商品は「単利」で運用することになります。
- 国債
- 社債
- 分配金を受け取るタイプの投資信託
- 銀行などの定期預金(単利型)
複利式とは
利子だけが増える単利式に対し、複利式では「利子が元本に組み込まれていき、元本が増える」という大きな違いがあります。
金利に変更がなくとも、元本の金額が増えるので、相対的に利子は毎年増額していくことになります。
いわば「利子で儲けた分を元手にしてさらに増やしている」「お金がさらにお金を生む」という状態であり、単利に比べると運用効果は高くなります。
つまり自身が長期で資産運用をする場合、複利式のほうが総合的に多くのお金を得られることになるというわけです。
事実、10万円を単利と複利で30年間運用した場合、金額に約1.7倍もの差が開くといわれています(年利5%で運用した場合)。かの有名なアインシュタインも「複利は人類最大の発明」と発言したことがあるくらい、投資をするうえでは欠かせない計算方法なのです。
- 定期預金(複利式)
- 株式
- 投資信託(再投資型)
単利と複利の計算式は?
自分の資産を単利または複利で運用するときは、まず計算をしてシミュレーションをしてみることが大切です。
ここでは単利、複利それぞれの利息計算式をご紹介します。
単利の利息計算式
単利式の場合、利息の計算はかんたんです。「元本×金利 = 利息(年間)」にて求められます。
仮に元本100万円、金利が1%だった場合、利息は100万円×0.01=1万円とます。元本+利息の合計額は1年目で101万円、20年積み立てた場合は120万円になっている計算です。
なお、定期預金の場合は預け入れの際に指定する「満期日」に利息が発生します。よって5年間預けた場合は、満期の日に1年ごとの利息×5年分を「満期日利息」として受け取れる、という仕組みです。
なお、金融商品によっては「3ヶ月もの年率5%の特別キャンペーン」というふうに、一定期間のみ高金利で商品を提供しているケースもあります。
この場合は「元本×金利÷12(ヶ月)×3(ヶ月)」という計算式で、金利アップ期間中の利息を計算できます。
複利の利息計算式
複利の場合の計算式はやや複雑で、「元本×{(1+年利)}年数の累乗」という式で元本を含む総額を計算できます。
仮に元本100万円、年利4%、20年間複利で運用した場合、計算式は100万円×(1+0.04)20 となり、20年後には219万1123円に増えている計算となります。
なお、複利の場合の計算は複雑になるため、CASIOが提供している「複利計算(元利合計)」などのサイトを利用するか、複利計算ができるスマートフォンアプリを活用するとわかりやすいでしょう。
参考リンク
複利計算(元利合計) – 高精度計算サイト|CASIO
「グラフで複利計算 | シンプルで簡単!」(iOS用)
簡単複利計算(Android用)
複利は「組み入れ期間」が短いと利子の総額が多くなる
単利は年利さえ同じならば、組み入れ期間(満期までの期間)が短くても長くても「受け取る利息の金額」に変化はありません。そもそも1年間の利息額が決まっているためです。
一方、複利に関しては組み入れ期間が短いほど利息総額が多くなります。
たとえば100万円を年利0.2%の複利型定期預金、6ヶ月定期で1年運用するとしましょう。
この場合1年間に2回利息を受け取れることになりますが、1回目・2回目それぞれの受取利息は
2回目:101万円×0.002÷12(ヶ月)×6(ヶ月)=約1,010円
1回目と2回目を合算すると2,010円となります。
単利の場合は同じ元本・年利であれば単純計算で2,000円の利息が付きますが、複利ならば若干利息額が多くなることをお分かりいただけるでしょう。
なお、上記は1年というごく短い期間で計算していますが、これが10年、20年…と年数が増えた場合は、複利のほうが圧倒的に有利です。次項では、複利で長期積み立ての資産運用をした場合のシミュレーションをご紹介します。
複利で積立するとどれくらいになる?複利計算のシミュレーション

何らかの金融商品を購入し、複利で積み立て投資をした場合はどのように利息が増えていくのでしょうか。
ここでは単利・複利それぞれの手法で「元本200万円、年利2%で10年間」運用したシミュレーションをしてみます。
【年利2%、単利式で投資した場合】
| 年数 | 元本の金額 | 利息額 | 利息の合計受取金額 |
|---|---|---|---|
| 運用スタート時 | 2,000,000円 | – | – |
| 1年目 | 2,000,000円 | 40,000円 | 40,000円 |
| 2年目 | 2,000,000円 | 40,000円 | 80,000円 |
| 3年目 | 2,000,000円 | 40,000円 | 120,000円 |
| 4年目 | 2,000,000円 | 40,000円 | 160,000円 |
| 5年目 | 2,000,000円 | 40,000円 | 200,000円 |
| 6年目 | 2,000,000円 | 40,000円 | 240,000円 |
| 7年目 | 2,000,000円 | 40,000円 | 280,000円 |
| 8年目 | 2,000,000円 | 40,000円 | 320,000円 |
| 9年目 | 2,000,000円 | 40,000円 | 360,000円 |
| 10年目 | 2,000,000円 | 40,000円 | 400,000円 |
上記の表のとおり、単利式では元本と年利が変わらない限り毎年定額で利息が増えていくことになります。10年目には40万円まで利息が増えています。
【年利2%、複利式で投資した場合】
| 年数 | 元本の金額 | 利息額 | 利息の合計受取金額 |
|---|---|---|---|
| 運用スタート時 | 2,000,000円 | – | – |
| 1年目 | 2,040,000円 | 40,000円 | 40,000円 |
| 2年目 | 2,080,800円 | 40,800円 | 80,800円 |
| 3年目 | 2,122,416円 | 41,616円 | 122,416円 |
| 4年目 | 2,164,864円 | 42,448円 | 164,864円 |
| 5年目 | 2,208,162円 | 43,298円 | 208,162円 |
| 6年目 | 2,252,325円 | 44,163円 | 252,325円 |
| 7年目 | 2,297,371円 | 45,046円 | 297,371円 |
| 8年目 | 2,343,319円 | 49,548円 | 343,319円 |
| 9年目 | 2,390,185円 | 46,866円 | 390,185円 |
| 10年目 | 2,437,989円 | 47,804円 | 437,989円 |
10年間の利息総額は437,989円と、単利式の場合(400,000円)に比べ約38,000円も多くなることがわかりますね。また、利息が元本に組み込まれていくぶん、利息額が徐々に増えていることも特長です。
複利で資産を2倍にするには何年必要? 72の法則・126の法則について
「複利で資産を2倍にするには何年くらいかかるのか」を知りたいとき、『72の法則』を使うとかんたんに計算ができるのをご存じでしょうか?
72の法則とはいわゆる「計算式」のことで、以下の計算をすればもともとの資産(元本)が2倍になる年数がわかります。
たとえば年利1%で資産を運用した場合、72÷1=「72年」の月日を要することになります。
一方、年利が6%だった場合は、72÷6=「12年」で資産が倍になる計算です。
また「72÷年数」で計算すれば、○年で資産を2倍にするために必要な年利(%)も算出可能です。
ちなみに、積み立て投資をする場合は「126の法則」という計算式で算出ができます。
たとえば年利6%で積立投資をした場合、126÷6=「21年」で資産を倍にすることができます。
複利計算をマスターして資産運用に役立てよう
投資で資産運用をする際は、複利の力を身につけることが非常に大切です。本記事でご紹介した複利の考え方、利息の計算方法などを把握しておき、効率よく資産運用を続けていきましょう。
ただし、投資(資産運用)はリターンがある一方、それぞれの金融商品にリスクがあることを忘れてはいけません。またそのリスク・リターンは金融商品によっても大きく異なるため、複数の金融商品を組み合わせ、リスクを分散させる対策も重要になります。
近年は銀行の預け入れ利率も過去最低レベルにあり、「銀行にお金を預ければ増える」という時代はもはや終わりに近いといえます。投資をされたことがない方は、本記事をきっかけにいま一度資産運用・投資について考えてみてはいかがでしょうか。